
Önce Mayın Tarlası ile başlayalım. Bilgisayar size kapalı karelerden oluşan bir ızgara gösterir. Bazı karelerin altında mayın vardır, diğerleri ise güvenlidir. Göreviniz mayınları patlatmadan hangi karelerin altında mayın olduğunu tespit etmektir. Bunun için de önce gelişigüzel bir kare seçersiniz. Eğer altında mayın varsa patlar ve oyun biter, kaybedersiniz. Eğer altında mayın yoksa o zaman bilgisayar o karenin içine bir sayı yazar ve bu sayı o kareye komşu olan sekiz karede (yatay, dikey ve çapraz) kaç tane mayın bulunduğunu gösterir.
Oyunda seçtiğiniz ilk karede bir mayına denk gelirseniz şansınız yok demektir: kaybettiğiniz bilgisi dışında bir bilgi edinemezsiniz. Ama eğer ilk denemede ölmezseniz yakınınızdaki mayınlara dair kısmi bilgi sahibi olursunuz. Bu bilgiden faydalanarak bir sonraki kareyi seçer ve açarsınız, sonuçta ya mayın patlar ya da az önce olduğu gibi açılan karenin civarındaki mayınların sayısı hakkında bilgi sahibi olursunuz. Dilerseniz bir kareyi mayın barındırıyor olarak işaretleyebilirsiniz: eğer yanılıyorsanız kaybedersiniz. Bu şekilde ilerlemek sureti ile alandaki tüm mayınları bulup işaretleyerek oyunu kazanabilirsiniz.

Şekil 1. Tipik bir Mayın Tarlası pozisyonu
Örneğin birkaç hamleden sonra Şekil 1'deki duruma gelebilirsiniz. Buradaki bayrak bilinen bir mayını (pozisyonu zaten belirlenmiş olan) gösterirken sayılar da bilgisayarın size verdiği bilgileri göstermektedir. Harfler ise henüz durumu belli olmayan, test edilmemiş kareleri belirtir. Biraz düşünerek altlarındaki 2 sayısından ötürü A harfi ile işaretlenmiş karelerde mayın bulunması gerektiğini çıkarabilirsiniz. B harfi ile işaretlenmiş karelerde de mayın olmalıdır yanlarındaki 4'ler ve 5'lerden ötürü. Benzer şekilde C karesinde bir mayın bulunmalı ve buradan mantık yürütürsek D ve E karelerinde mayın olmamalı. F ile işaretlenmiş karenin durumu, birkaç hamle sonra D'yi açıp hangi sayı çıktığına bakarak belirlenebilir.
Şimdi de P=NP? problemine gelelim. Algoritmanın ne olduğunu hatırlayın, bilgisayar tarafından çalıştırılabilen ve bir problemi çözmeye yarayan prosedür: prosedürün her adımı bir program tarafından belirlenir. Bilgisayar bilimlerindeki temel sorulardan biri şudur: bir algoritma belli bir problemi ne kadar etkin şekilde çözebilir? Yani algoritmanın çalışma zamanı - cevaba erişmek için gerçekleştirilmesi gereken hesap sayısı - başlangıçta girilen veri ile ne şekilde ilişkilidir? Teorik bakımdan temel ayrım, P tipi problemler - polinom zaman - ile böyle olmayanlar arasındadır. Eğer bir problem, çalışma zamanı başlangıç verisini belirlemek için kullanılan sembollerin sayısının sabit bir kuvvetinden daha hızlı büyümeyen bir algoritma ile çözülebiliyorsa P tipindendir. Aksi takdirde P-olmayan tiptendir. Sezgisel olarak bakarsak, P tipi problemler etkin şekilde çözülebilirken P-olmayan problemler algoritmik olarak pratik şekilde çözülemezler çünkü cevaba ulaşmak herhangi bir algoritma ile saçma derecede uzun sürer. P tipi problemler kolayken P-olmayan problemler zordur. Tabii ki mesele bu kadar basit değildir ama kısaca böyle hatırlayabiliriz.
Bir problemin P tipi olduğunu, o problemi polinom zamanda çözen bir algoritma bularak ispatlayabilirsiniz. Örneğin bir sayı listesini sayısal olarak sıraya dizmek P tipi problemdir, ticari veri tabanları bu sayede veriyi hızlıca sıralayabilirler; bir karakter katarında başka bir karakter katarını aramak da P tipi problemdir, kelime işlemciler bu sayede bul ve değiştir türü işlemleri kolayca yapabilmektedir. Bunlardan farklı olarak Seyahat Eden Satıcı Probleminin - bir seyahat planına göre her şehri ziyaret etmesi gereken satıcı için en kısa yolu bulun - P-olmayan türden olduğu düşünülmektedir ancak bu henüz ispatlanamamıştır. Bir tamsayının asal çarpanlarını bulmanın da P-olmayan olduğuna inanılmaktadır ancak bu da henüz ispatlanmamıştır. Internet üzerinden kredi kartı gibi hassas kişisel bilgilerin gönderilmesinde kullanılan bazı şifreleme sistemlerinin güvenliği bu inancın doğru olduğu düşüncesine dayanmaktadır.
Bir problemin P tipi olmadığını ispatlamak neden bu kadar zordur? Çünkü bunu belli bir algoritmayı analiz ederek yapamazsınız. Tüm olası algoritmaları tasarlamanız ve bunlardan hiçbirinin problemi polinom zamanda çözemediğini göstermeniz gerekir. Bu da afallatıcı zorlukta bir iştir. Bugüne kadar gelinen en iyi nokta P tipi olmadığı düşünülen problemlerden oluşan geniş bir sınıfın üyelerinin birbirlerine denk olduklarını ispatlamak olmuştur - yani eğer bunlardan biri polinom zamanda çözülebiliyorsa diğerleri de polinom zamanda çözülebilir. Burada bahsedilen problemlerin 'belirlenemez polinom' (nondeterministic polynomial) çalışma zamanı olduğu söylenir: NP tipi.
NP, P olmayan demek değildir. Eğer bir problem için önerilen çözümün gerçekten de çözüm olup olmadığını polinom zamanda kontrol edebiliyorsanız o zaman bu NP tipi problemdir. Bu, çözümü polinom zamanda bulmaya kıyasla çok daha gevşek bir koşuldur. Konunun daha iyi anlaşılması için kullandığım favori örnek yapbozdur. Yapboz türü bulmacayı çözmek çok zor olabilir ama eğer birisi yapbozu çözdüğünü iddia ederse bunun doğru olup olmadığını kontrol etmek kolaydır, çözüme şöyle bir bakmanız yeterlidir. Çalışma zamanına dair sayısal bir fikir edinmek isterseniz sadece sırayla her parçaya bakın ve etrafındaki sınırlı sayıdaki komşusu ile uyuşup uyuşmadığını kontrol edin. Bunu yapmanız için gereken hesaplama sayısı kabaca elinizdeki parça sayısı ile doğru orantılıdır, dolayısı ile çözümün kontrolü polinom zamanda gerçekleşir. Ancak yapbozun kendisini bu şekilde çözemezsiniz. Her çözümü sıra ile deneyemezsiniz de çünkü potansiyel çözümlerin sayısı yapbozu oluşturan parçaların sayısının sabit herhangi bir kuvvetinden çok daha hızlı artar.
Pek çok NP tipi problemin birbirlerine 'denk' çalışma zamanına sahip olduğu görülmüştür. Daha detaylı söylemek gerekirse: Eğer bir NP problem için bulunabilecek çözüm polinom zamanlı ise ve bu tüm NP problemlerin polinom zamanlı çözümleri olması gerektiğini gösteriyorsa o zaman o probleme NP-tam denir. Birini polinom zamanda çözün, tümünü polinom zamanda çözmüş olursunuz. Pek çok problemin NP-tam olduğu bilinmektedir. P=NP? problemi ise P ile NP tipindeki problemlerin aslında aynı kategoride olup olmadıklarını sorar (böyle olmadıklarına dair görünürdeki tüm ipuçlarına rağmen). Beklenen cevap 'hayır'dır. Ancak bir NP-tam problemin P tipi problem olduğu ortaya çıkarsa - yani polinom zamanlı çözümü bulunduğu - o durumda NP ile P birbirlerine eşit olmalıdır. Bu yüzden tüm NP-tam problemlerin P olmayan tipte olduklarını sanıyoruz ancak hiç kimse henüz bunu ispatlayamadı.
Bilinen en basit NP-tam problemlerden biri de bir Boole şartının mantıksal olara sağlanması problemidir (SAT). Boole devreleri VE (AND), VEYA (OR) ve DEĞİL (NOT) gibi isimleri olan mantık kapıları ile oluşturulur. Bu devrelerin girdisi T (True; (D (doğru))) veya F (False (Y (yanlış))) olabilir. Her kapı belli sayıda girdi alır ve bunların kombinasyonunun mantıksal değerini çıktı olarak verir. Örneğin bir VE kapısı p ve q girdilerini alıp p VE q çıktısını üretir ki bu da p ve q aynı anda DOĞRU ise DOĞRU aksi takdirde YANLIŞ demektir. Bir DEĞİL kapısı DOĞRU girdisini alıp YANLIŞ ve YANLIŞ girdisini alıp DOĞRU çıktısını üretir. SAT problemi şunu sorar: Verili bir Boole devresi için DOĞRU çıktısını üretecek girdiler kümesi var mıdır? İlk okuyuşta kolay geldi ise hatırlatalım ki bir devrede çok fazla kapı ve girdi olabilir.

Şekil 2. İmkansız Mayın Tarlası pozisyonu
Bu problem ile Mayın Tarlası oyunu arasındaki bağlantı Mayın Tarlası Tutarlılık Problemini tanıttığımızda kurulmaktadır. Bu sefer problem mayın bulmak değil verili bir Mayın Tarlası pozisyonunun gerçekten de geçerli yani oyunda karşılaşılabilecek bir pozisyon olup olmadığını belirlemektir. Örneğin oyunu oynarken Şekil 2'deki gibi bir durumla karşılaşırsanız programcının bir hata yaptığını anlarsınız: gösterilen bilgilerle uyumlu bir mayın dağılımı söz konusu olamaz. Kaye, birazdan tarif edeceğimiz bakımdan Mayın Tarlasının SAT problemine denk olduğunu ispatlamıştır. Verilen bir Boole devresi için tanımlanmış SAT problemi, bir Mayın Tarlası Tutarlılık Problemi, yani oyundaki bir pozisyon olarak 'kodlanabilir' (bu dönüşümü gerçekleştiren prosedür polinom zamanda çalışmaktadır). Dolayısı ile eğer Mayın Tarlası Tutarlılık problemini polinom zamanda çözebilirseniz söz konusu devre için SAT problemini de polinom zamanda çözebilirsiniz. Başka bir deyişle, Mayın Tarlası NP-tamdır. O halde, eğer zeki biri Mayın Tarlası için polinom zamanlı bir algoritma bulursa veya böyle bir çözümün olmadığını ispatlarsa P=NP? problemi de (öyle ya da böyle) çözülmüş olur.
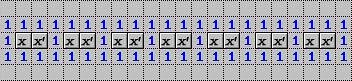
Şekil 3. Bir Mayın Tarlası teli
Kaye'in kanıtı Boole devrelerini Mayın Tarlası pozisyonlarına dönüştürmek için sistematik bir prosedür içerir. Burada bir ızgara karesi eğer mayın içeriyorsa T, içermiyorsa F durumundadır. İlk adım mantık kapılarını değil onları birbirine bağlayan telleri içerir. Şekil 3'te bir Mayın Tarlası teli görülmektedir. x ile işaretlenmiş kareler ya bir mayın içerir (T) ya da mayın içermez (F) ama hangi durumun geçerli olduğunu bilmeyiz. x' ile işaretlenmiş kareler, x ile işaretlenmiş karelerin tersidir. x ile işaretlenmiş bir karenin T mi F mi olduğunu belirlemek için gösterilen tüm numaraların doğru olup olmadıklarını kontrol etmeniz gerekir. Telin etkisi T ya da F sinyalini tel boyunca taşımak ve bir kapıya girdi olacak şekilde hazırlamaktır.
Şekil 4'te bir DEĞİL kapısını görülebilir. Ortadaki blokta işaretlenmiş sayılar girdi teline göre çıkış telinde x ve x' olanların birbirleri ile değişmesini sağlar.
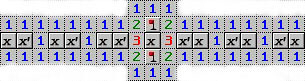
Şekil 4. DEĞİL kapısı
Şekil 5'teki VE kapısı daha karmaşıktır.
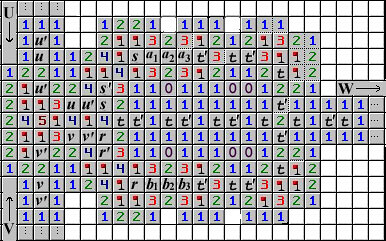
Şekil 5. VE kapısı
Burada U ve V isimli iki girdi teli ve W isimli bir çıktı vardır. Bunun bir VE kapısı olduğunu belirlemek için çıktının T olduğunu ve her iki girdinin de T olduğunu var sayıyoruz. Çıktı T olduğu için her t sembolü bir mayınlı kareyi ve her t' sembolü de bir mayınsız kareyi göstermeli. O halde a3'ün üstünde ve altındaki 3 sayısı a2 ve a3'ün mayın olduğunu gösterir, dolayısı ile a1 mayın olamaz ve buradan da s'nin mayın olduğu çıkar. Benzer şekilde r mayındır. O halde merkezdeki 4'ün zaten dört komşusu mayın olduğuna göre u' ve v' mayın değildir dolayısı ile u ve v mayındır - ki bu da U ve V'nin T doğruluk değerine sahip olduğu anlamına gelir. Tersine eğer U ve V, T doğruluk değerine sahipse W de öyledir. Kısaca en başta iddia ettiğimiz gibi elimizde bir VE kapısı vardır.
Mayın Tarlası elektroniği ile ilgili bu anlatılanlardan daha fazlası var - örneğin telleri bükebilmemiz, ayırabilmemiz, birleştirebilmemiz ve birbirlerine değmeden birbirleri üzerinden geçirebilmemiz gerekir. Kaye tüm bu problemleri ve daha incelikli olanlarını makalesinde bahsettiği yöntemle çözmektedir. Sonuç olarak Mayın Tarlası Tutarlılık Problemi SAT problemine denktir, dolayısı ile NP-tamdır. Bu da tüm matematikçiler ve bilgisayar bilimciler için bu problemin doğal olarak çok zor olduğu anlamına gelir. Bu kadar basit görünen bir oyunun böylesine ele avuca sığmaz sonuçlara yol açması şaşırtıcıdır fakat işte bazı matematiksel oyunlar böyledir.
Eğer bu milyon dolarlık ödüllerle ilgileniyorsanız sizi önceden uyarayım. Clay Enstitüsü bir çözümü geçerli kabul etmek için bazı sıkı kurallar koymuştur. Çözümünüz hakemli bir matematik dergisinde yayımlanmalı ve o andan itibaren 2 sene içinde matematik camiası tarafından 'genel olarak kabul edilmiş' olmalıdır. Bu işe girişmeyecekseniz bile Mayın Tarlası oynayıp bu programın çağımızdaki en büyük çözülmemiş problemlerden birini barındırdığını düşünerek eğlenebilirsiniz.
Prof. Dr. Ian Stewart
Clay Matematik Enstitüsü, bu makalenin web sitemizde yayımlanmasına izin verdiği için Ian Stewart'a teşekkür eder.
Mayın Tarlası oyunu ve P=NP? problemi arasındaki bağlantı ile ilgili daha detaylı bilgi Birmingham Üniversitesi'nde çalışan Richard Kaye'in kişisel web sitesinde bulunmaktadır:
http://web.mat.bham.ac.uk/R.W.Kaye/minesw/minesw.htm. Richard Kaye'in sitesinde "Some Minesweeper Configurations" (Bazı Mayın Tarlası Konfigürasyonları) başlıklı makale de mevcuttur.
* : http://www.claymath.org/Popular_Lectures/Minesweeper/ adresindeki metinden Emre Sevinç tarafından, 20-24 Ağustos tarihleri arasında çevrilmiştir ;-). Ian Stewarta çeviri ve yeniden yayımlama iznini verdiği için teşekkür ederiz.
Çeviri için teşekkürler çok güzel bir yazı.
Ancak küçük bir eleştirim var; keşke yazının çeviri olduğu bilgisi ve orjinal adresi en altta değil de en başta olsaydı. Ben orjinalinden okumayı tercih ederdim... eğer bilseydim.