Nasıl kesmeli?

Geçtiğimiz hafta Festival of the Spoken Nerd ekibi tarafından düzenlenen An Evening of Unnecessary Detail başlıklı etkinliğe katıldım. Etkinlik boyunca dokuz farklı gösteri sergilendi fakat bunlardan bir tanesi özellikle diğerlerinden farklı olarak kendini gösteriyordu. Burada onunla ilgili birşeyler paylaşmak istedim.

Elinizde bir A4 kağıt olduğunu düşünün, ve bu kağıttan bir kare kesmeniz gerekiyor. Sadece elinizde bir kare kalması değil, aynı zamanda A4 kağıdın da ortasında kare şeklinde bir boşluk kalmasını hedefliyorsunuz. Nasıl kesersiniz? Bu sorunun cevabı oldukça basit. A4 kağıdı katlayıp aşağıda göründüğü şekilde keserseniz bir kare elde edebilirsiniz ve A4 kağıdınızda da o şekilde bir boşluk oluşur.

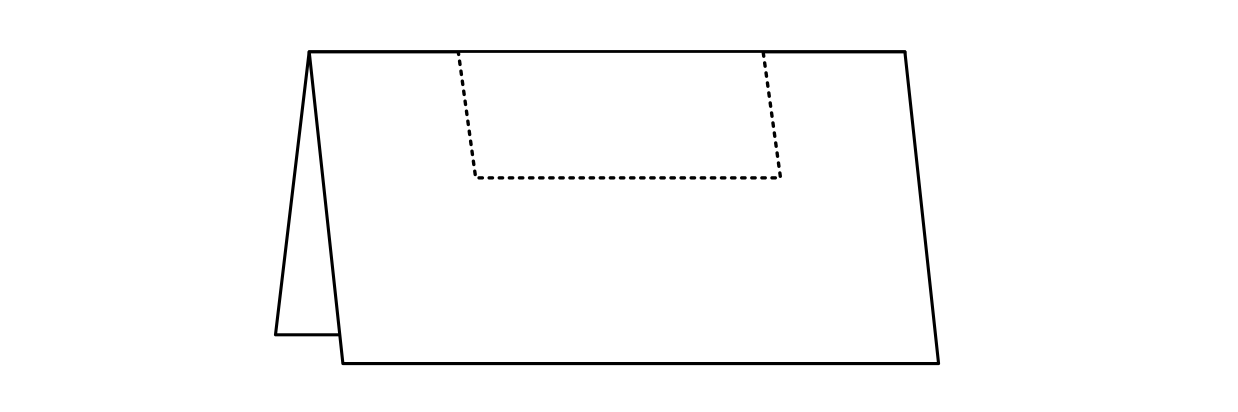
Harika! Peki ama ya benim gibi elinizin ayarı olmayan bir insansanız? O üç kenardan yapacağınız kesiklerin birbirini tutmasının imkanı olmadığını tahmin edebilirsiniz. Peki çare? Çare yapılacak kesik sayısını azaltmaktan geçiyor tabi ki. Kağıdı bir defa daha katlayarak aşağıdaki hale getirdiğinizde iki kesikle kurtulmanız mümkün.

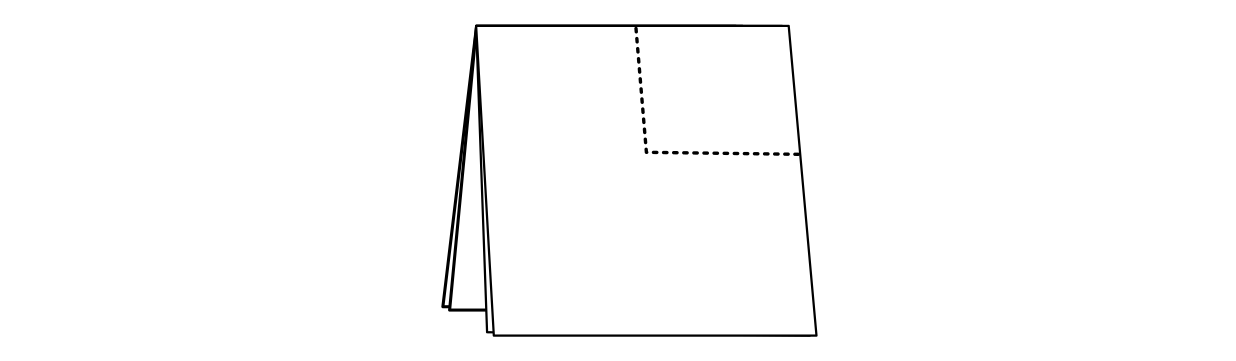
Peki buradan nereye gideceğimizi tahmin edebilen var mı? Evet, eğer bunu buraya kadar getirebildiysek aşağıda gördüğünüz şekilde uygun bir katlama ile tek bir kesiğe de indirgeyebiliriz.

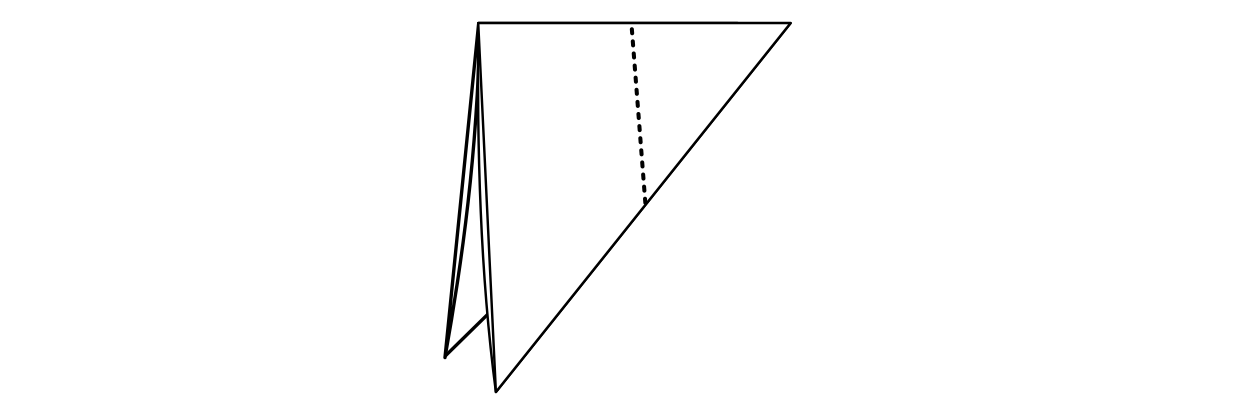
Evet, artık elinizin ayarı ne kadar bozuk olursa olsun bir kağıttan tek bir kesikle bir kare kesebilirsiniz. Aramızda derdi sadece kare kağıt kesmek olanlar burada okumayı bırakabilir. Bırakmayanlar ise bir şekilde matematikle ilgilenen insanlardır diye tahmin ediyorum. Etkinlikte bu sunumu yapan Katie Steckles da bu noktada durmamış ve şu soruya takılmış: peki kare dışında hangi şekilleri bu yöntemle, tek bir kesikle üretebiliriz? Araştırmaları kendisini Erik Demaine'in bu konudaki çalışmalarına ulaştırmış. Kısaca söylemek gerekirse, sorunun cevabı: Sadece düz kenarlardan oluşan her şekli bir kağıdı doğru şekilde katlayıp tek kesikte üretmek mümkün.

Bunun üzerine bu konu hakkında çalışmaya başlayan Katie Steckles İngiliz alfabesinin bütün harflerini bu şekilde üretmeyi başarmış. Çalışamasının sonuçlarını bu videoda görebilirsiniz.

Bence bu durum doğru koşullar (Katie Steckles'in durumunda kendisi gibi matematikçilerle rahat bir şekilde etkileşime girebileceği bir pub) sağlandığında basit bir "aaa ne ilginç" tepkisinin nasıl bilimsel bir çalışmaya dönebileceğinin güzel bir örneği. Gerek bilim, gerek teknoloji üretmek konusunda olsun doğru zamanda, doğru topluluk içinde bulunmanın insan hayatını kökten değiştirebileceğine yaşayarak şahit olmuş bir insanım.

Siz ne düşünüyorsunuz? Verimli bir üretim süreci için doğru topluluk içinde yer almak şart mı? Yoksa o "cevher" bir insanın içinde varsa bir şekilde ortaya çıkar mı?

Kapak görseli